My Research
My research interest sits at the intersection of applied mathematics, data science, and scientific modeling, with a focus on solving real-world problems through quantitative tools. I’m particularly interested in systems where data, uncertainty, and theory all intersect, biological processes, environmental modeling, and complex physical systems. Whether I’m working on plant growth or quantum information, I aim to build models that are both mathematically sound and practically useful.
Across all of my work, I try to maintain a balance between curiosity-driven inquiry and application-focused research. I enjoy asking how we can use modeling to inform better decisions, whether it’s in agriculture, energy systems, or public health. Going forward, I’m especially interested in contributing to collaborative, interdisciplinary projects that use data and modeling to address complex challenges in science, policy, and the environment.
Crop Per Drop: Mathematically Modelling the Growth of Dark Red Kidney Beans
Current trends in farming are pressuring growers to generate higher crop yields with fewer resources. This pressure necessitates embracing precision agriculture,
using data and science-based practices that are targeted at the micro-environments on the field level, to increase a grower’s overall efficiency. Chippewa Valley
Bean (CVB), located in Menomonie, Wisconsin is the world’s largest processor of dark red kidney beans and works with growers all over Wisconsin and the Upper
Midwest. Their agronomy team is looking to incorporate more precision agriculture to help their growers deliver higher yields of higher quality beans.
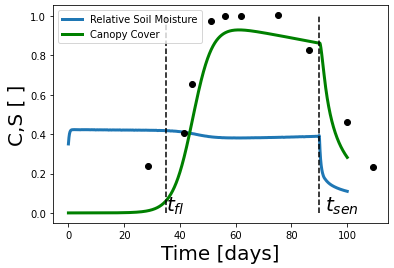
CVB’s agronomy team tasked us with determining the amount of water required to grow dark red kidney beans in different soil types. We developed a mathematical model
consisting of three coupled differential equations tracking water in the soil, canopy, and total reproductive biomass throughout a kidney bean plant’s life cycle. This
model serves to predict the total yield of a plant given the irrigation levels as well as the characteristics of the plant and soil type. We then used numerical experiments
to identify the irrigation levels that give the maximum kidney bean yield.
You can find media on this project here and here!
Magic Labeling of Zero Divisor Graphs
The magic square problem is a classic mathematical puzzle that involves arranging numbers in a square grid so that the sums of each row, each column, and both main diagonals are all equal. A magic square of order \(n\) is a \(n \times n \) matrix filled with distinct integers (typically from 1 to \(n^2\)) such that the sum of each row, column, and diagonal is the same magic constant, given by:
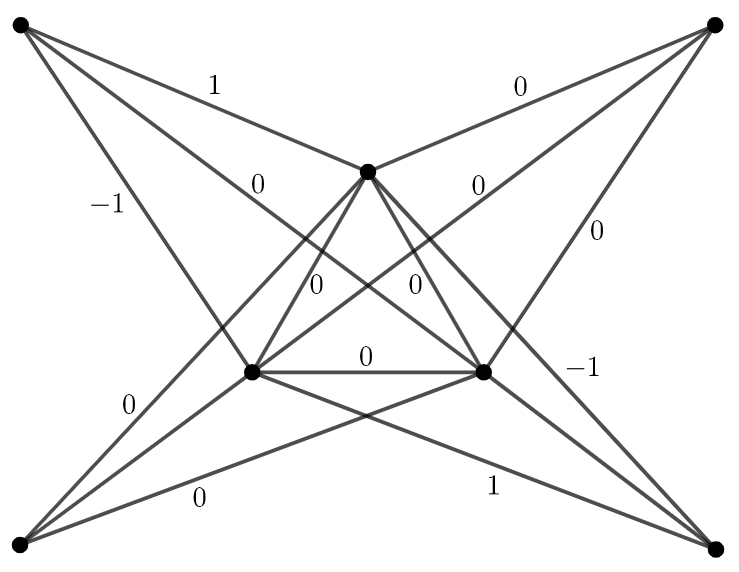
\[ M = \frac{n(n^2+1)}{2} \] In this paper, we investigate magic type labelings of zero-divisor graphs, focusing on semi-magic, magic, and super-magic labelings. We construct infinite families of commutative
rings that admit these labelings, as well as families that do not. Additionally, we classify the magic type properties of all zero-divisor graphs with up to 14 vertices.
A key result is the identification of conditions under which a commutative ring's zero-divisor graph is semi-magic, magic, or super-magic. We find that while many graphs admit semi-magic
labelings, only specific forms (such as certain complete and complete bipartite graphs) are magic or super-magic. The paper concludes with several open conjectures regarding the extension
of these patterns to larger graphs.
This work builds upon previous studies of zero-divisor graphs and contributes to the broader study of graph labelings, particularly in algebraic settings.
You can find the paper here!